In a five-part series in his blog, Functional Finance and the Debt Ratio Scott Fullwiler claims that if the interest rate is held below the growth rate of output, sustainability of the public debt/gdp ratio is guaranteed in the sense that the ratio converges and does not keep increasing forever. This is erroneous and his conclusions are misleading.
Wolfgang Schäuble understands the connection between public finances and international competitiveness, although his solutions are all wrong. Heteredox economists should understand this connection as well!
Rather than write a detailed essay, I thought I should directly get to the point and pinpoint his errors. Of course, several Post Keynesians even before Fullwiler wrote his 2006 paper Interest Rates And Fiscal Sustainability (referred in his posts) have made this claim and this criticism applies to them as well.
While there are future scenarios, where growth improves the public debt/gdp ratio, it does not mean that all scenarios lead to a convergence. Fullwiler has examples in his posts where he shows how the convergence happens. But it doesn’t prove much.
Fullwiler’s error is a simple mathematical one. He sums the series for debt-sustainability equation and shows the the public debt/gdp ratio converges to
– pb/(g – r)
where pb is the primary balance/gdp ratio, g is the growth rate of output and r the interest rate. [notations are changed somewhat without any effect on conclusions]
This is a wrong result because it assumes that the primary balance is constant as a percentage of gdp. The series he sums need not converge if the primary balance in each period is different. One such scenario is when the deficit in each period is bigger than the deficit of the previous period. Fullwiler claims:
… in terms of convergence or unbounded growth of the debt ratio, as Jamie Galbraith put it, “it’s the interest rate, stupid!” since any level of primary deficit can converge if the interest rate is below the growth rate.
[italics and link in original]
This is repeated:
… More importantly, given an interest rate lower than GDP growth, any primary budget deficit will eventually converge …
Now this doesn’t make sense. The claim that “any” level of primary deficit can converge if the interest rate is below the growth rate is incorrect. For example, if we have primary balances pb0, pb1, pb2 and so on and each of them is growing sufficiently faster, the debt/gdp ratio is explosive even if interest rate is less than the growth rate of output. His result is valid if each of the balances pb0, pb1, pb2 … are equal to each other and not in general.
In other words, if g>r, the sequence dn given by the relation
dt – dt-1 = λdt-1 – pbt
where λ is equal to (r-g)/(1+g) need not converge for general values of pbn and only converges in special circumstances (if suppose the pbn are all equal or more realistic if there is a mechanism to bring the primary deficit into a surplus which may or may not be a discretionary attempt by the government.)
Example
Nothing of the above is purely academic. So in what situation can the public debt explode?
Let us assume an open economy. Let us assume that a country’s exports is X0 and not growing because of its inability to increase its market share or because of limited demand in world markets due to deflationary policies adopted by the rest of the world. Or both.
If one imagines a scenario in which there is growth in output and hence income, imports rise as well in a world of free trade. This implies the current account deficit explodes. While growth may work to improve the debt/gdp ratio, the current account deficits work to worsen the debt ratio. The net effect is that “growth” instead of improving the debt/ratio worsens it.
This can be seen if one remembers that the sectoral balances identity connects the public sector deficit and the current balance of payments. We have
NAFA = PSBR + BP
where NAFA is the private sector net accumulation of financial assets, PSBR is the public sector borrowing requirement (the deficit) and BP is the current account balance of international payments.
Since the private sector typically wishes to have a positive NAFA (else there is another unsustainable process!), an exploding BP leads to an exploding PSBR if output grows much faster than exports. This implies the public debt/gdp grows forever and growth is not sustainable.
Now Fullwiler can potentially claim that the government can “simply credit bank accounts” and public debt/gdp and external debt/gdp rising forever is no cause for trouble but then why write a post claiming convergence of the ratios!
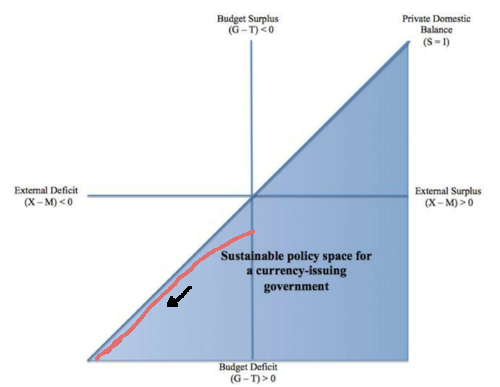
There is a diagram in the post which I modified below with a red line for a path for the sectoral balances. Is the claim that this line extrapolated leads to a stabilizing debt ratio?
Wynne Godley And Debt Dynamics
The above was pointed out by Wynne Godley in the 1970s. The following brings it out clearly. It is from an appendix to an article written by his co-author Bob Rowthorn in J. Michie and J. Grieve Smith (eds), Unemployment in Europe (London: Academic Press), 1994 pp. 199-206 and was originally a paper to the UK Treasury around ’92-’93
Conclusion
Now this may sound as a pessimistic view for any individual nation or the world as a whole. The real problem is free trade – the most sacred tenet of the economics profession.